You stumble across the ruins of an ancient castle...

The ruins of the castle have left a strange pillar formation behind. In particular, there are ~N~ adjacent pillars each with height ~h_i~. Let ~x~ represent your exhaustion. It initally starts at ~1~, and increases by ~1~ after each time you jump to a taller pillar. It takes ~x~ seconds to travel from pillar ~i~ to pillar ~i+1~ if ~h_i \ge h_{i+1}~. However, there are ~2~ different ways to travel to a taller pillar.

You can run across pillar ~i~ in ~x~ seconds and then climb up to pillar ~i+1~ in ~x(h_{i+1}-h_{i})~ additional seconds.

Alternatively, you can jump directly from pillar ~i~ to pillar ~i+1~ in ~x~ seconds. You can jump as high as you want, but jumping will exhaust you.

Given this information, what is the lowest amount of time needed to get from pillar ~1~ to pillar ~N~?

Constraints

~2 \le N \le 2000~

~1 \le h_i \le 10^5~

Subtask 1 [40%]

~2 \le N \le 20~

Subtask 2 [60%]

No additional constraints.

Input Specification

The first line of input contains an integer ~N~.

The second line of input contains ~N~ space separated integers representing ~h_i~, the height of each pillar.

Output Specification

Output a single integer, the lowest achievable time in seconds.

Sample Input

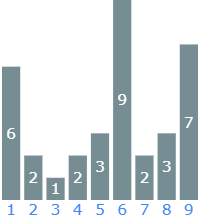
9
6 2 1 2 3 9 2 3 7

Sample Output

14

Sample Input Visualized