Shahir was already taped shut in the box when it occurred to him that he didn't know if it was possible to get from his house to his prom date's. That's no problem: he asks one of the friends that will deliver him, Dhruvit, to check.

There are ~N~ houses in Shahir's neighbourhood, and ~M~ roads that connect those ~N~ houses. Each road connects two houses. All roads can be traveled down both directions. Each house is distinctly numbered and identified by a number in the range ~1..N~.

Shahir lives in house ~A~. His date lives in house ~B~. Is there a path of roads to follow such that Dhruvit can drive the packaged Shahir from house ~A~ to house ~B~? Dhruvit wrote (and you, vicariously, will write) a program to answer that question.

Input Specification

The first line will contain four integers, separated by spaces:

• ~N~ ~(1 \leq N \leq 2000)~: The number of houses in Shahir's neighbourhood.
• ~M~ ~(0 \leq M \leq N)~: The number of roads in Shahir's neighbourhood.
• ~A~ ~(1 \leq A \leq N)~: Shahir lives in house A.
• ~B~ ~(1 \leq B \leq N)~: Shahir's date lives in house B.

The next ~M~ lines contain two space-separated integers ~X~ and ~Y~ ~(1 \leq X, Y \leq N)~, denoting a road that connects house ~X~ with house ~Y~. Two roads will never connect the same two houses.

Output Specification

On a single line, print GO SHAHIR! if Shahir can make it to his date's house. Otherwise, print NO SHAHIR!.

Sample Input 1

6 7 1 6
1 2
2 3
2 5
5 1
3 4
4 5
4 6

Sample Output 1

GO SHAHIR!

Explanation for Sample 1

Here is the graph of Shahir's neighbourhood:

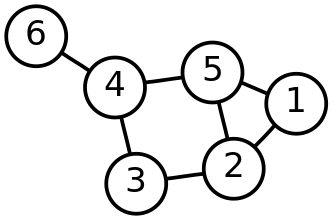
Shahir's house is house ~1~. His date's house is at house ~6~. Dhruvit can drive Jeffrey from houses ~1~ to ~6~ by following the path ~1, 2, 3, 4, 6~ or ~1, 5, 4, 6~.

Sample Input 2

6 6 1 6
1 2
2 3
2 5
5 1
3 4
4 5

Sample Output 2

NO SHAHIR!

Explanation for Sample 2

This map of Shahir's neighbourhood is the same as the one in Sample 1, but the edge between houses ~4~ and ~6~ is removed. As a result, Dhruvit can no longer drive Shahir to his date's house.